La gamme chromatique | Jacques Rougemont

J’aimerais examiner en détail la construction de la gamme chromatique et les problèmes d’intonation qu’elle pose, à l’aide de la représentation ci-dessous.

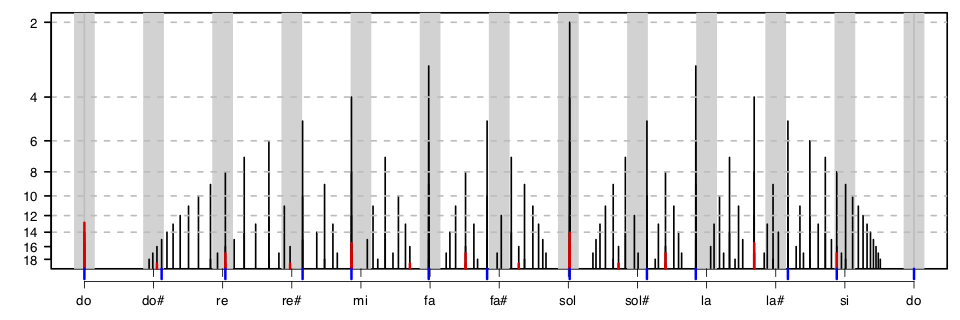
Figure 1: La gamme chromatique et le problème de l’intonation. L’échelle horizontale représente les fréquences espacées logarithmiquement, l’échelle verticale la consonance relative au do (les plus petits dénominateurs sont en haut de l’échelle). Les bandes grises représentent $\pm 15$ cents autour des notes tempérées. Les lignes noires verticales sont tous les rapport rationnels de dénominateur inférieur à $19$.

Les 12 demi-tons divisent l’octave en 12 intervalles égaux sur une échelle logarithmique (axe horizontal de la figure). Comme illustration, je prends une fréquence arbitraire que j’appelle do$_0$ et les fréquences successives $2^{1/12}$ plus élevées (environ 6%) jusqu’à la fréquence double: le do$_1$ à l’octave. Les zones grises autour de chaque demi-ton représentent un écart de ±15 cents: ce sont les notes “accessibles” (pour les instruments à cordes, à vent, les chanteurs, etc.). Chaque ligne noire verticale indique un intervalle consonant par rapport au do$_0$ grave: plus la ligne monte haut plus l’intervalle est consonant (l’axe vertical représente le dénominateur du rapport des fréquences). Les intervalles “justes” sont indiqués par les tirets bleus. Les harmoniques de do sont indiquées par des tirets rouges (plus petits si la fondamentale correspondante est plus grave).

Par exemple, la quinte (sol) chromatique (tempérée) est à la fréquence $2^{7/12}\approx 1.4983$, ce qui est très proche de la quinte juste (rapport de $3/2=1.5$) qui est aussi une harmonique du do$_{-1}$ une octave plus bas. On constate qu’il n’y a aucun autre intervalle consonant dans le voisinage de ce sol et que ce rapport de $3/2$ est le plus consonant de tous. On en déduit que la quinte est non ambiguë (facile à chanter) et consonante (dans un rapport de fréquences très simple).

Première remarque générale: les harmoniques (rouge) ne tombent pas toujours sur des intervalles justes (bleu). Il y a bien un rapport entre série harmonique et impression de consonance, mais ces harmoniques ne fournissent pas les notes de la gamme de manière directe. Observez en particulier la quarte juste (fa): c’est un intervalle non ambigu et consonant mais il ne se trouve pas dans la série harmonique (sauf bien sûr comme complémentaire de la quinte juste: intervalle du sol au do dans la série harmonique de do).

Examinons maintenant quelques situation musicalement instructives: la tierce majeure (mi) est proche de deux intervalles consonants: $5/4$ qui est nettement plus bas ($13.69$ cents) et $19/15$ ($9.24$ cents plus haut). On en déduit que la tierce majeure sonne mal sur un clavier (car l’intervalle tempéré est loin des intervalles justes), elle est très consonante (dénominateur $4$) mais légèrement ambiguë (difficile à accéder et en conflit avec un autre intervalle moins consonant: dénominateur $15$). A l’autre extrémité, la seconde mineure (do#) n’a que des intervalles peu consonants à proximité (dénominateurs plus grands que $15$). Le rôle de cet intervalle dans la gamme est purement mélodique (par symétrie) et non harmonique. Un autre cas intéressant est celui de la sixte majeure: la (fréquence $2^{9/12}\approx 1.68$) qui peut être considérée comme proche du rapport $5/3$, mais l’écart est de $15.64$ cents, ce qui est à la limite de l’atteignable selon les instruments. Encore plus problématique est la septième mineure la# ($2^{10/12}\approx 1.78$) qui est proche de plusieurs intervalles plutôt consonants: $9/5,16/9,23/13,25/14$, mais le meilleur ($9/5$) est aussi le plus éloigné ($17.60$ cents). Il y a donc une forte ambiguïté sur cette note, ce qui signifie que le musicien aura des difficultés à trouver l’intervalle juste et sera attiré par des intervalles moins harmoniques, mais plus proches.

Pour illustrer ces difficultés voici quelques intervalles mentionnés ci-dessus:

Tierce majeure