Prenons deux ondes sinusoïdales pures (des fondamentales sans harmoniques) de fréquences $\omega_1 < \omega_2=\omega_1+\delta$. Leur superposition peut s’écrire
\begin{eqnarray}
\phi_{\omega_1}(t)+\phi_{\omega_2}(t)&=&
\alpha\cos(2\pi\omega_1 t)
+\beta\cos(2\pi\omega_2 t+\tau)\nonumber\\
&=&
\Bigl(\alpha^2+\beta^2+2\alpha\beta\cos(2\pi\delta t+\tau)\Bigr)^{1/2}
\cos(2\pi\omega_1 t+\psi(t))~,
\end{eqnarray}
avec un déphasage défini par $\tan(\psi(t))=\frac{\sin(2\pi\delta t+\tau)}
{\alpha/\beta+\cos(2\pi\delta t+\tau)}$.
On obtient donc une note de fréquence $\omega_1$ modulée (en amplitude et en phase) avec une fréquence $\delta$ qui est la différence $\omega_2-\omega_1$ entre les deux fréquences initiales.

Plusieurs cas sont intéressants à considérer:

• $\omega_2=k\omega_1$. Dans ce cas, la modulation est exactement à la même fréquence qu’une harmonique de l’onde elle-même, le battement n’existe pas.
• $\frac{\omega_2}{\omega_1}=\frac pq\in\mathbb{Q}$. La fréquence du battement ($\frac{p-q}{q}\omega_1$) et la fréquence fondamentale ($\omega_1$) sont des multiples de $\frac{\omega_1}q$, donc toutes les fréquences font partie d’une même série harmonique: on a une onde périodique.
• $\frac{\omega_2}{\omega_1}\in\mathbb{R}\setminus\mathbb{Q}$. La fréquence de modulation et la fondamentale sont incommensurables, le résultat est une onde non périodique (ce n’est pas une note identifiable).
• $\omega_2=\omega_1+\epsilon$. La longueur d’onde de la modulation est $1/\epsilon$ [s]. Si $\epsilon$ est suffisamment petit (de l’ordre de $10$ [Hz]) on entend alors clairement les battements dans l’intensité du son (voir Figure 2 ci-dessous).

Remarquez qu’en pratique on ne peut distinguer un rapport strictement irrationel d’un rapport dont le dénominateur est grand, donc la distinction entre périodique (spectre discret harmonique) et quasi-périodique (spectre discret non harmonique) n’est pas essentielle.

Lorsque les ondes possèdent des harmoniques, on obtient la situation suivante (en notation complexe et sans les déphasages $\tau_n$):
\begin{eqnarray*}
\phi_{\omega_1}(t)+\phi_{\omega_2}(t)&=&
\sum_{n=0,1,2,\dots}\Bigl( \alpha_ne^{2i\pi n\omega_1 t}+\beta_ne^{2i\pi n\omega_2 t} \Bigr)\\
&=&\sum_{m=0}^\infty e^{2i\pi mp\omega_1 t}
\Bigl(\alpha_{mp}+\beta_{mq}+\sum_{n=1}^{p-1}\alpha_{mp+n}e^{2i\pi n\omega_1 t} +\sum_{n=1}^{q-1}\beta_{mq+n}e^{2i\pi n\omega_2 t}\Bigl)
\end{eqnarray*}
Chaque multiple $n\frac pq$ peut être décomposé en partie entière et fractionnelle:
$$
n\frac pq\,=\,\left[n\frac pq\right]+\epsilon_n\,=\, k_n+\frac{\ell_n}q~,
$$
où $0<k_n<p$ et $0<\ell_n<q$ sont des entiers. Donc on peut reformuler la dernière somme ci-dessus comme:
\begin{eqnarray*}
&&\sum_{n=1}^{q-1}\left( \frac{\ell_n}q\beta_{mq+n}e^{2i\pi\frac{\ell_n}q\omega_1 t} e^{2i\pi k_n\omega_1 t} +\frac{q-\ell_n}q\beta_{mq+n}e^{-2i\pi\frac{q-\ell_n}q\omega_1 t} e^{2i\pi(k_n+1)\omega_1 t} \right)\\
&=&\sum_{k=1}^{p-1}\left(\gamma_{mp+k}e^{2i\pi\frac{\ell_{mp+k}}q\omega_1 t} +\gamma_{mp+k}’e^{-2i\pi\frac{\ell_{mp+k}’}q\omega_1 t}\right) e^{2i\pi k\omega_1 t}~, \end{eqnarray*}
où certains coefficients $\gamma_n, \gamma_n’$ et $\ell_n, \ell_n’$ sont nuls. Finalement on trouve:
\begin{eqnarray*}
\phi_{\omega_1}(t)+\phi_{\omega_2}(t)
&=& \sum_{n=0,1,2,\dots}\Bigl( \alpha_n +\gamma_ne^{2i\pi\frac{\ell_n}q\omega_1 t}+\gamma_n’e^{-2i\pi\frac{\ell_n’}q\omega_1 t} \Bigr)e^{2i\pi n\omega_1 t}~. \end{eqnarray*}
Autrement dit chaque harmonique de la note grave est modulée en amplitude et en phase avec des fréquences multiples de $\omega_1/q$. Il existe d’ailleurs toujours certaines harmoniques dont la modulation est exactement à la fréquence $\omega_1/q$.

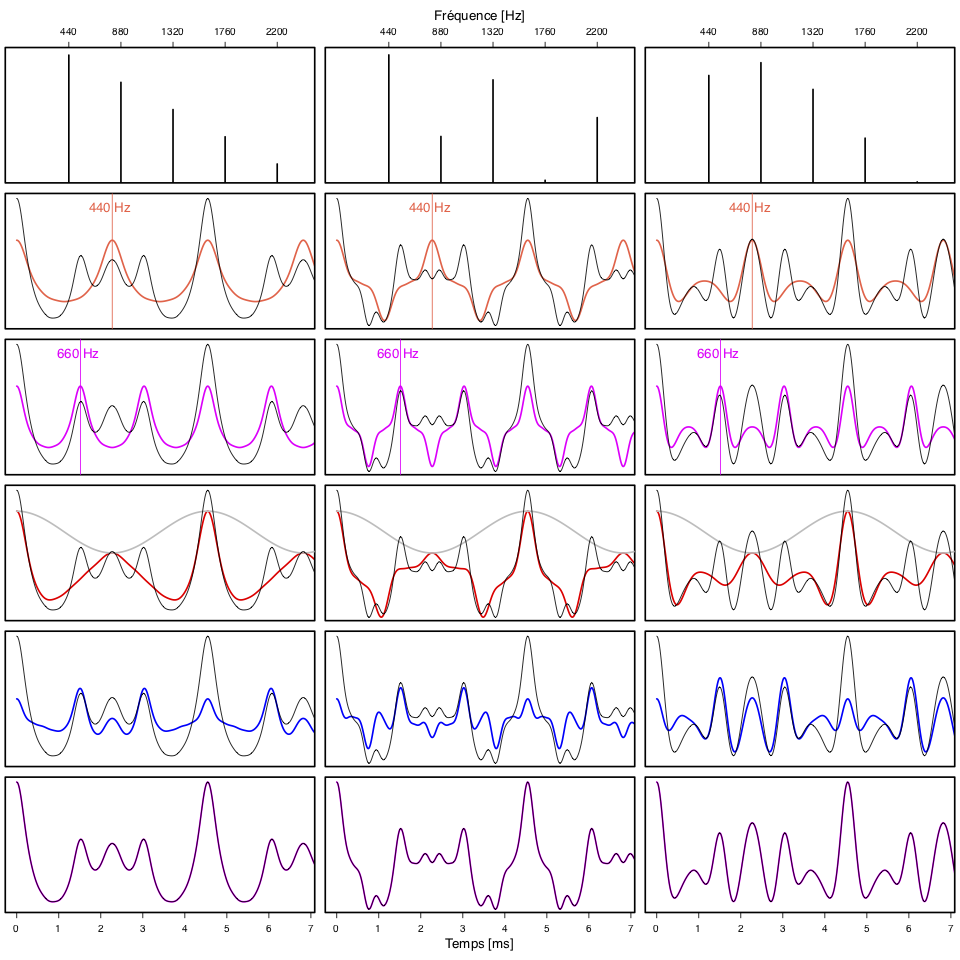
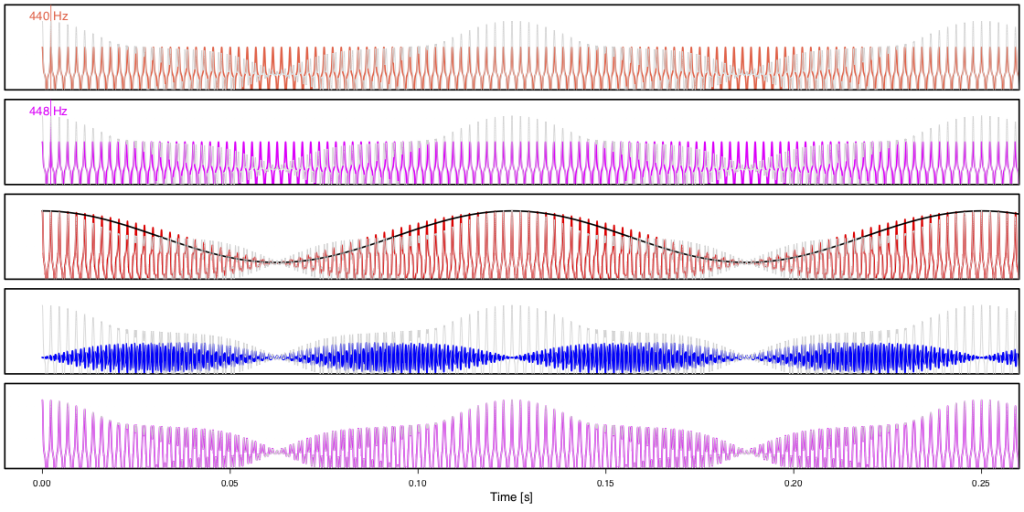
La Figure 1 ci-dessus illustre les différents termes de cette décomposition pour trois spectres de fréquences différents (représentés sur la 1ère ligne, les fréquences indiquées au-dessus correspondent à une fondamentale à 440 [Hz]). Sur chaque panneau, la courbe noire représente la somme de deux ondes de même spectre et de fréquence fondamentale 440 [Hz] (la) et 660 [Hz] (mi). Les lignes 2 et 3 montrent les ondes individuelles (en orange le la, plus grave, en rose le mi, plus aigu). Le terme principal est en rouge (4e ligne) avec l’enveloppe de fréquence $660-440=220$ [Hz] en gris. Les termes de hautes fréquences sont en bleu (5e ligne), et la somme des signaux bleu et rouge (6e ligne en violet) est bien égale à la courbe noire qui est la somme des deux ondes individuelles. La même décomposition s’applique à la superposition de deux notes proches (un la à 440 [Hz] et un la “désaccordé” à 448 [Hz], Figure 2). On observe alors un battement à 8 [Hz].

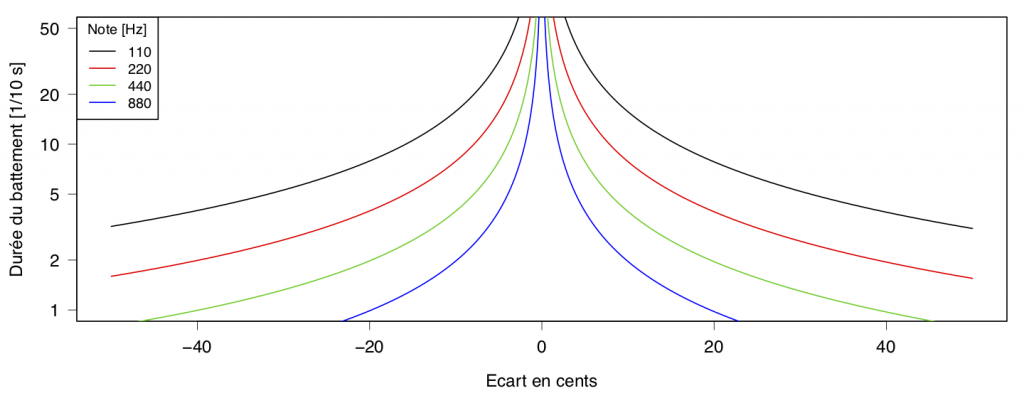
Comme illustration pratique, remarquez que l’on peut déduire l’écart en cents entre deux notes en écoutant la fréquence des battements qu’elles produisent. Par exemple deux notes à $440$ [Hz] et $442$ [Hz] (7.85 cents d’écart) produisent des battements de 5 dixièmes de secondes.

Vous pouvez écouter les sons représentés dans la Figure 1 (2ème colonne, la 440 Hz et mi 660 Hz) et dans la Figure 2 (mélange 440 Hz et 448 Hz) ci-dessous: