On trouve fréquemment dans la littérature la formule trigonométrique suivante pour expliquer le phénomène des battements: $$\cos(\omega_1 t)+\cos(\omega_2 t)=2\cos(\frac{\omega_1-\omega_2}2 t)\cos(\frac{\omega_1+\omega_2}2t)~,$$ avec l’interprétation que le premier facteur est l'”amplitude” du battement (de fréquence $\Omega=(\omega_1-\omega_2)/2$) qui module l’oscillation (le second facteur) de fréquence $\overline\omega=(\omega_1+\omega_2)/2$).
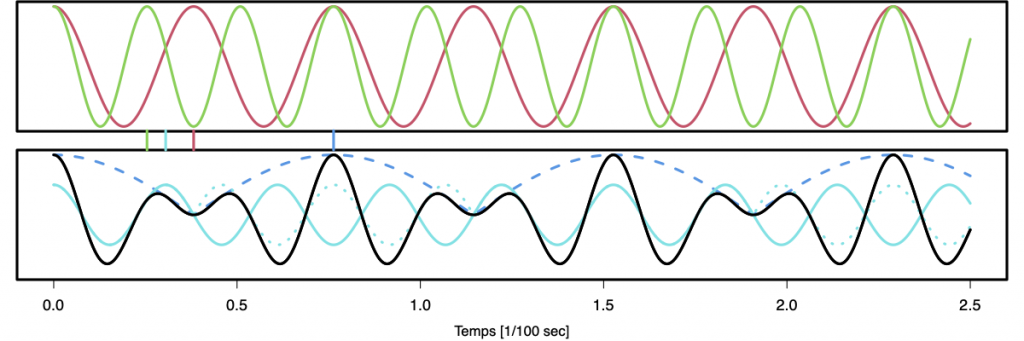
Cette formule est bien entendu mathématiquement correcte, mais pose un certain nombre de problèmes dans son interprétation:
- Il n’y a aucune généralisation naturelle de cette formule à la somme de deux ondes d’amplitudes différentes, c’est à dire: $A\cos(\omega_1 t)+B\cos(\omega_2 t)$ avec $A\ne B$.
- Elle n’a en réalité pas la forme Amplitude$\times$Oscillation, car une amplitude est une fonction non-négative. L’interprétation visuelle de cette décomposition est d’ailleurs plutôt comme $$|\cos(\Omega t)|\times\mbox{sign}(\cos(\Omega t))\cos(\overline\omega t)~.$$ Remarquez que la fréquence de $|\cos(\Omega t)|$ est $2\Omega$!
- Ces formules trigonométriques sont des identités exactes, donc valables aussi bien pour des petites différences $\omega_1-\omega_2$ que des grandes différences (deux notes différentes). Il semblerait donc que l’addition d’un Do (262 Hz) et d’un Sol (393 Hz) serait alors un Mi (327.5 Hz) avec un battement à 65.5 Hz (trop rapide pour être entendu). Ceci n’est musicalement pas vrai: on n’entend pas Mi, mais bien Do.
