On a discuté ci-dessus la gamme chromatique comme “réservoir” de notes dont on extrait les gammes. Mais pourquoi diviser l’octave en 12 demi-tons, plutôt que 9 (cf. la gamme pelog), 20 (certaines gammes indiennes) ou, pour les amateurs de science-fiction, 42?

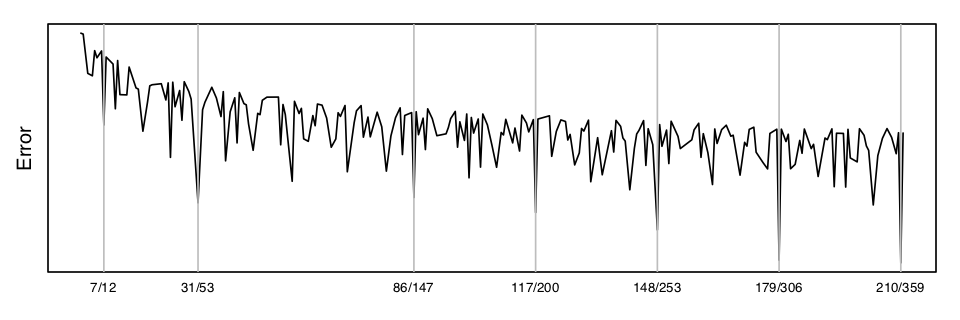
Ce choix peut-être justifié ainsi: on veut certainement inclure dans notre gamme l’intervalle de la quinte juste (rapport $3/2$) car il est le plus harmonique. Malheureusement on ne peut produire cette quinte à l’aide d’une division égale de l’octave car $$\log_2(3/2)=0.5849625007211\dots$$ est un nombre irrationnel: aucune fraction entière de l’octave ne peut le représenter. On peut par contre trouver de bonnes approximations: $7/12=0.58\overline3, 31/53=0.5849057\dots, 86/147=0.58503401\dots$, etc. (voir ci-dessous).

Pour chaque approximation, son erreur produit une “quinte du loup”: par exemple 12 quintes successives tombent $12\log_2(3/2)-7=0.01955\dots$ ($23.46$ cents) plus haut que $7$ octaves. En accordant les $12$ demi-tons d’un instrument, ces $23.46$ cents doivent être répartis d’une manière ou d’une autre entre ces $12$ notes. Si, naturellement, on commence par do et on accorde chaque quinte successive vers le haut (sol, ré, la,…) et le bas (fa, si♭, mi♭,…) au rapport exact de $3/2$, on termine avec un intervalle fa♯–do♯ trop court de $23.46$ cents.

On aurait pu diviser l’octave en 53 parts égales et n’avoir qu’une erreur de 3.615 cents à répartir. La gamme indienne discutée précédemment utilise précisément certains intervalles très proches de la fraction $1/53$ de l’octave (mais tous ne sont pas autorisés). D’un autre côté la gamme pelog est construite sur une division de l’octave en 9 parties qui ne donne qu’une mauvaise approximation de la quinte juste.