La plupart des personnes (non entraînées) ont des difficultés à déterminer si deux notes jouées successivement sont égales ou légèrement différentes, mais peuvent pourtant reconnaître avec une grande précision lorsque des notes jouées simultanément sont identiques, à l’octave ou dans un rapport fractionnel simple [Oppenheim (2013), LoPresto (2015), McDermott (2010), VanHedger (2018), Jacoby (2019), Loosen (1995)]. Cela provient du fait discuté ci-dessus que les harmoniques coïncident où non, produisant parfois des battements audibles. On peut exprimer cela en disant que lorsque le rapport entre deux fréquences est un nombre rationnel avec un petit dénominateur (comme pour les intervalles diatoniques), la combinaison des ondes est une série harmonique incomplète dont manque, en particulier, la fondamentale.
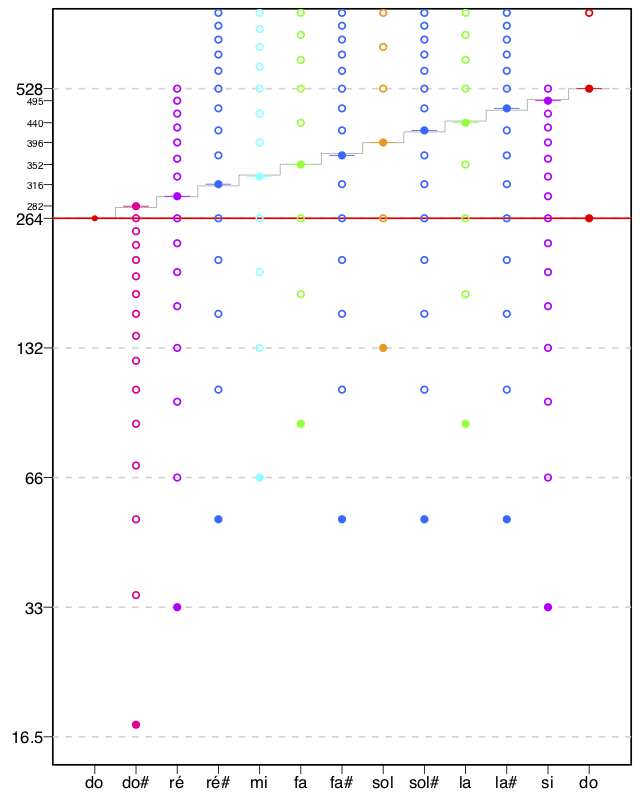
Les compositeurs classiques ont établi une classification des intervalles du plus consonant au plus dissonant (voir Table 1). On peut schématiser en disant que plus la fondamentale virtuelle est éloignée, plus l’accord est considéré comme dissonant. La Figure 1 montre pour chaque note de la gamme chromatique quelle série harmonique contient à la fois cette note et le do inférieur.
| Consonance | Intervalle | Fondamentale virtuelle |
|---|---|---|
| +++ | Octave | 1 |
| ++ | Quinte j. | 2 |
| (+) | Quarte j. | 3 |
| + | Sixte maj. | 3 |
| + | Tierce maj. | 4 |
| + | Tierce min. | 5 |
| (- -) | Quarte aug. | 5 (18) |
| + | Sixte min. | 5 |
| – | Septième min. | 5 |
| – | Seconde maj. | 8 |
| – – | Septième maj. | 8 |
| – – | Seconde min. | 15 |
Mathématiquement, on considère deux fréquences $\omega_2>\omega_1$ dans un rapport rationnel: $\omega_2/\omega_1 = p/q$ (fraction irréductible). On a donc une fondamentale virtuelle $\omega_0=\omega_1/q$ et on peut voir que la première harmonique commune à ces deux fréquences est $\omega_3=q\omega_2$. On peut donc “entendre” cette résonance entre les deux notes d’autant mieux que $q$ est petit.
On peut étendre ce raisonnement aux accords, tels que triades et tétrades. Par exemple une triade peut être représentée par le triplet $(1, p/q, m/n)$ (on factorise la fréquence de la note basse) et l’harmonique commune sera donc le plus petit entier multiple de $p/q$ et $m/n$, par exemple les trois triades suivantes:

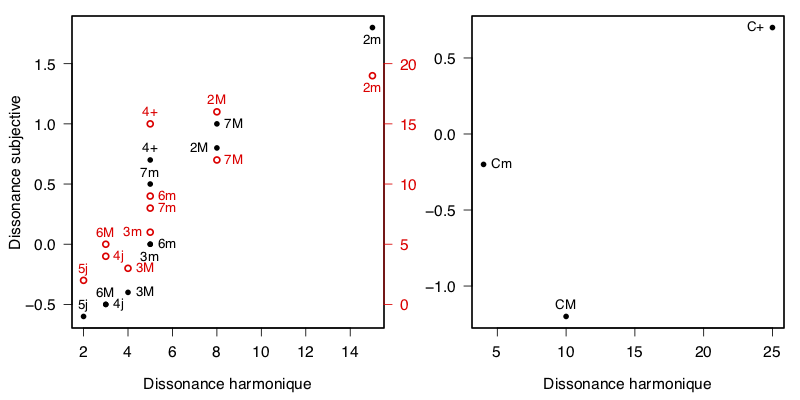
(majeure: $(1,5/4,3/2)$, mineure: $(1,6/5,3/2)$ et augmentée: $(1,5/4,8/5)$) ont des degrés de consonance de, respectivement 10, 4, et 25 (harmonique commune aux trois notes, comptée depuis la quinte).
Des données expérimentales montrent que l’impression subjective de consonance corrèle avec cette mesure, sachant que les tests ont été réalisés sur des assemblages de sons synthétiques (donc des intervalles chromatiques) et que l’accord mineur, par exemple, sonne plus dissonant que le majeur si les tierces ne sont pas “justes” (si elles sont tempérées).